동전 두 개를 붙여서 돌렸을 때 몇 바퀴 회전하는가?
오늘은 정말 쉬워보이지만 맞추기 어려운 문제를 가져왔다.
문제

사진과 같이 동전이 2개 있다.
동전이 서로 붙어있는 상태에서 아래있는 동전의 원 둘레를 따라 위에 있는 동전을 굴린다.
위에 있는 동전이 아래 동전을 한 바퀴 돌아서 다시 제자리에 왔을 때
위에 있는 동전은 몇 바퀴를 회전했을까?
정답
정답은 당연히 1바퀴? 라고 생각했으면 틀렸다.
정답은 2바퀴다.
문제풀이

1바퀴라고 생각한 사람은 아마도
원의 크기를 다르게 냈다면
이러한 풀이를 했을 것이다.
반지름으로 각각의 원의 둘레를 구하고 비교를 했을 것이다.
위의 그림 2개를 아래 그림처럼 합쳤을 때를 생각해보자.
원의 둘레 길이만큼을 한 번 이동하고
90도로 꺽인 방향으로 한 번 더 이동했을 때
원은 2바퀴를 돈 것에 빨간색 거리만큼 더 이동한다.

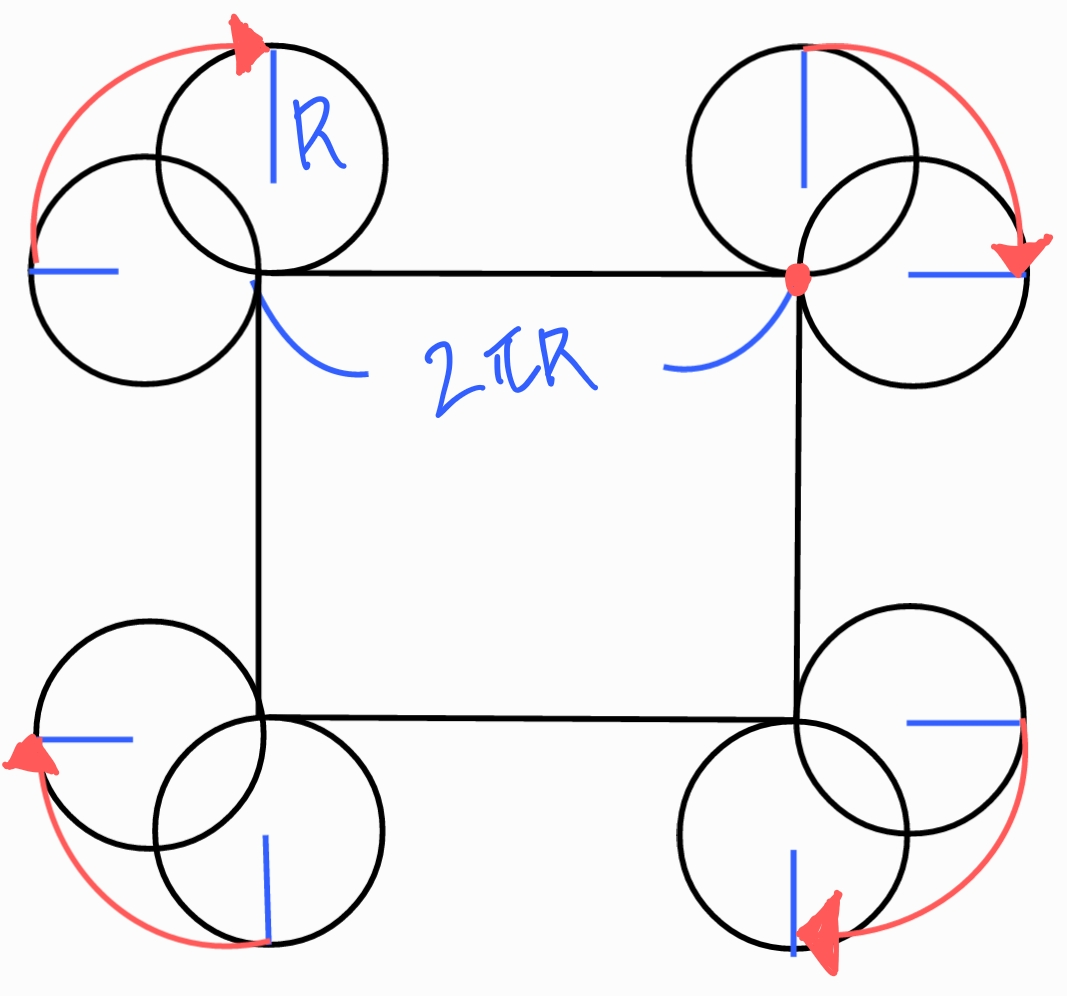
결국 한 변이 원의 둘레만큼인 정사각형이 있을 때
원이 굴러서 제자리에 오려면
네모의 둘레에 해당하는 원 4바퀴에
모서리에서 1/4 원에 해당하는 빨간색 회전을 총 4번한다.
즉 원이 한바퀴 다 돌았을 땐
우리가 생각하는 바퀴수에 +1을 하면 정답이 된다.
만약 네모가 아니라
오각형이라면 모서리에서 1/5 원 회전을 5번 하게 된다.
즉, 아무리 많은 다각형이어도 결국 더해지는 회전수는 1번이 된다.
아니면 육각형, 칠각형 ...... 무수히 많은 다각형이라면?
결국 원은 변이 무수히 많은 다각형이므로
다시 처음 문제로 돌아가서 문제를 풀면
동전의 둘레는 서로 같으므로 1바퀴 회전에
빨간색 회전에 해당하는 1바퀴를 더해서 2바퀴가 된다.
만약 R=1인 원이, R=3인 원 주위를 굴러간다면
총 3바퀴에 1바퀴를 더해서 4바퀴가 정답이 된다.
다른 문제 풀이
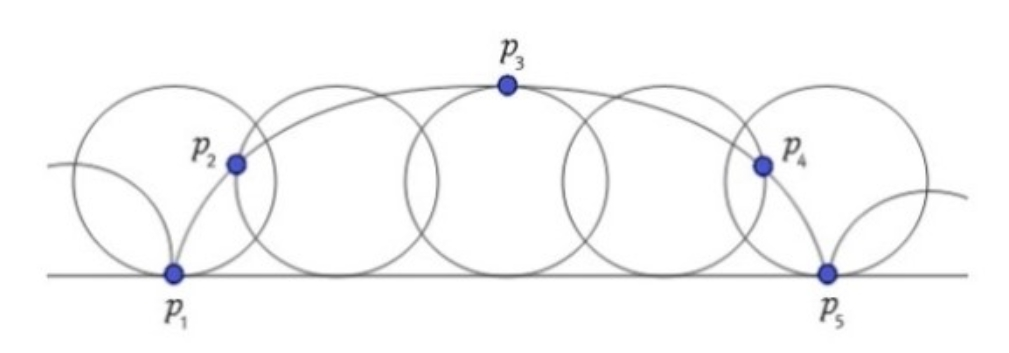
위 사진은 사이클로이드 곡선을 나타낸 것이다.
일정한 반지름을 갖는 원 위에 한 점을 찍고
원을 한 직선 위에서 굴렀을 때
점이 진행하면서 그리는 곡선이다.
P1에서 P2, P3, P4를 지나 P5에 도착하면
원이 한 바퀴 회전한 것을 의미한다.
그렇다면 원이 이동한 거리는 2πR이 된다.
그러나 점 P에 입장에서는 더 먼 거리를 이동했다.
우리가 흔히 말하는 이동한 거리는
원의 중심 입장에서 이야기한 것이다.

위 사진의 자전거 바퀴를 예시로 들면 이해가 쉽다.
자전거 바퀴가 한 바퀴 회전했을 때
중심 ㄱ은 원의 둘레 만큼 이동했지만
중심보다 떨어진 ㄴ은 더 먼 거리를 이동했고
ㄷ은 가장 많은 거리를 이동했다.
여기에서 우리는 한 가지 중요한 사실을 알 수 있다.
원의 중심을 기준으로 실제 이동 거리를 측정하고
이를 원의 둘레로 나누면 회전한 바퀴 수를 알 수 있다.
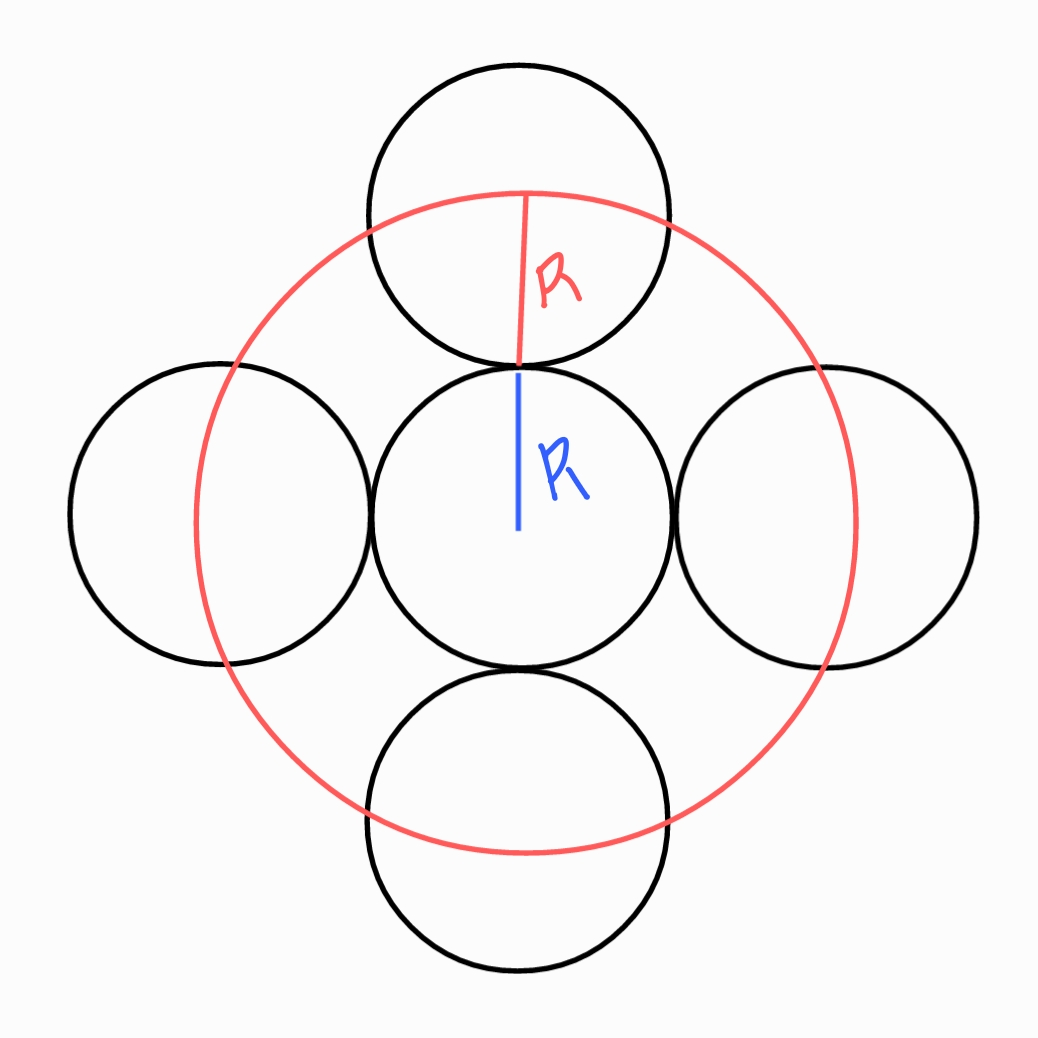
그럼 다시 문제로 돌아가보자.
반지름이 같은 원 두개가 있을 때
바깥쪽 원의 중심이 이동한 거리는
빨간 원의 둘레로 4πR이 된다.
즉 안쪽 원 둘레 2πR 보다
2배 더 많은 거리를 이동한 셈이다.
회사에서 우연히 듣게 된 간단한 퀴즈였는데
생각보다 정답을 이해하는데 꽤 시간이 소요됐다.
천문학을 하는 과학자들은 이러한 개념이 매우 친숙하다고 한다.
실제로 우리는 지구의 한 중심에 사는 것이 아닌
지구의 외각에 위치하기 때문이다.
지식이 늘어 갈수록 과학자들이 내심 존경스럽다.
'깨알정보' 카테고리의 다른 글
| 바람의나라 클래식 - 격술(2인) 사냥 가이드 (6) | 2025.03.03 |
|---|---|
| 삼성페이는 되고 애플페이는 안되는 이유? (0) | 2024.04.14 |
| 보조배터리 용량 (0) | 2023.11.19 |
| 거지키우기1 공략 (필수과금, 초중반 공략) (3) | 2023.08.01 |
| 수영장 부력 (0) | 2023.07.02 |













